A few weeks ago, Matt Parker released a video where he posed a question he’d received from a viewer about the popular game Wordle: how many words can you try in a Wordle game without reusing a letter? At most, the answer can be 5 (25 letters total with one unused). So the question becomes: are there sets of five English words without any overlapping letters, and (while we’re at it) if so, how many?
To answer this, Parker used a relatively naive approach that took about a month to run on an extra laptop. Quite a few clever people have since optimized their solutions to run much faster. In particular, Parker provided a link to Benjamin Paasen’s method, which used graph theory to bring the running time down to just over 20 minutes.
Essentially, the problem of finding sets of non-overlapping words can be reframed as finding a fully-connected subgraph in a network where all nodes are words and edges connect words which share no letters. By fully-connected, I mean that every node (word) has an edge (i.e. shares no letters) with every other word in that part of the network. In graph theory, these groups are known as cliques and there are a number of algorithms for finding them.
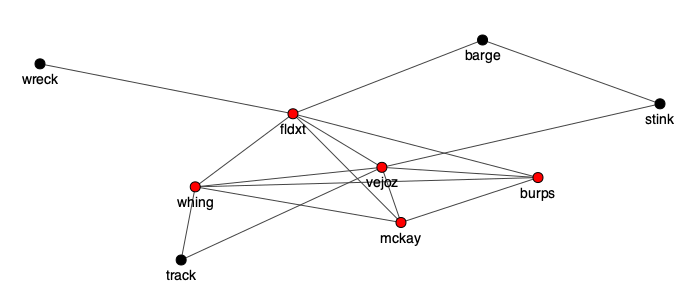
Passen implemented a method that builds cliques by searching neighbors for intersections of progressively more words. I thought we’d give the same approach a try, but see if we can take advantage of Python’s fantastic ecosystem – namely, the igraph package – to further improve the speed. First, we’ll need to recreate the set of words from which to search for five-word cliques. I used Parker’s source for all English words: the words_alpha.zip file which can be found here.
Preparing the Word List in (Functional) Style
After downloading the zip archive, we can load the words as an iterable using the zipfile library:
import zipfile
from pathlib import Path
from typing import Dict, Iterable, List, Tuple
def extract_archive_to_word_list(
archive_path: Path, filename: str
) -> Iterable[str]:
"""
Provided a path to a zip archive and the name of the file within the
archive containing an english word list, extract and read the file
and return an iterable of the words.
"""
return (
zipfile.ZipFile(archive_path, 'r')
.read(filename)
.decode('utf-8')
.split("\r\n")
)
Now, we have a series of filtering operations to do to select only 5 letter words without duplicate letters and to keep only one word from word sets which contain the same letters. I’ll use the pipe package to make each function work with shell-style piping to avoid creating intermediate variables.
from pipe import Pipe
@Pipe
def filter_words_of_length_n(words: List[str], n: int) -> Iterable[str]:
"""Filter out words not of length n."""
return filter(lambda word: len(word) == n, words)
@Pipe
def filter_words_with_duplicate_letters(words) -> Iterable[str]:
"Filter out words with more than one of any letter."
return filter(lambda word: len(word) == len(set(word)), words)
@Pipe
def filter_duplicate_word_sets(words: Iterable[str]) -> Iterable[str]:
"""Filter out words with the same set of letters as an already seen word."""
seen = set()
seen_add = seen.add
for word in words:
wordset = frozenset(word)
if wordset not in seen:
seen_add(wordset)
yield word
By filtering our word list with each of these functions, we can keep only words of length 5 which have no duplicate letters and remove any words that share all letters with words previously seen in the list. (For example, “create” and “react” share the same letters, so we’ll just choose one to include since the other will share all of the same cliques.) Thanks to the @Pipe decoration, each of these operations can be chained together with the | operator (which calls the next function on the result of the previous one):
@Pipe
def get_unique_set_words_of_length_n(
words: Iterable[str], n: int
) -> Iterable[str]:
"""Get the filtered list of words of length n with no repeating digits,
omitting any words with duplicate letter sets."""
return (
words
| filter_words_of_length_n(n)
| filter_words_with_duplicate_letters
| filter_duplicate_word_sets
)
Note that the
@Pipedecorator curriesfilter_words_of_length_nso that it can be called once for each of its arguments. The first argument is presumed to be the iterable, so calling the function withn=5returns a partial function with thenparameter pre-filled.
Ok, with that done, we can move on to creating our graph.
Building a Graph with iGraph
The igraph package provides a powerful Python interface to its optimized-C core graph routines, which we can use to find our 5-cliques. Creating an igraph.Graph object requires a list of all of the edges in the graph identified by tuples of vertex indices. (The constructor will infer the nodes from this list.)
import itertools as it
from igraph import Graph
def create_graph_of_disjoint_words(words: Iterable[str]) -> Graph:
"""
Create a igraph.Graph where each vertex is a word and two words
share an edge if they have no letters in common.
igraph.Graph takes a list of edges as tuples of vertex indices.
The edges are created by iterating through each word and adding
edges for any remaining words that have disjoint letter sets.
"""
wordsets = list(map(set, words))
edges = [
(i, j)
for i, left in enumerate(wordsets)
for j, right in it.islice(enumerate(wordsets), i+1, None)
if left.isdisjoint(right)
]
return Graph(edges = edges)
To create our list of vertices, we iterate through each of the words and add a tuple of node IDs (indices corresponding to the each word’s position in the word list) where the letter sets of the two words are disjoint (i.e. they don’t share any letters). Starting from the beginning of the word list, we check only the remaining words in the list for disjoint pairs each time to avoid rechecking the pairs of words (in reverse order).
Passing this edge list to igraph.Graph instantiates a graph with a node for each of the words in our word list with edges between words with disjoint sets of letters.
Finding all the Cliques
igraph.Graph has a cliques() method which will return cliques between a minimum and maximum size. Under the hood, this method calls the C method igraph_cliques(), which makes use of the Cliquer library written largely by Patric Östergård.1 For our purposes, finding cliques of a certain size is as simple as specifying the same lower and upper bound:
def find_all_size_n_cliques(
words: Iterable[str], size: int
) -> Iterable[Dict[int, Tuple[str, ...]]]:
"""Provided an iterable of strings, return all of the sets of words
of a given size with no overlapping letters between any pair in the set."""
_words = list(words)
graph = create_graph_of_disjoint_words(_words)
for pos, clique in enumerate(graph.cliques(size, size)):
yield {pos: tuple(_words[idx] for idx in clique)}
Note: Here, we call
list()on thewordsiterable since we’ll need it multiple times. (Otherwise, the iterable may be exhausted if it is a generator.)
I like using jsonlines as a serialization format, so I’ve formatted each set of words as a dictionary with the clique index as the key and the tuple of words as the values. (The cliques algorithm returns the node indices, so we have to recover the original words).
Lastly, we can write can create a main function that will write the results of this search to a jsonl file.
PARENT_DIR = Path(__file__).parent
WORDS_ARCHIVE_PATH = PARENT_DIR / "words_alpha.zip"
WORDS_FILENAME = "words_alpha.txt"
CLIQUES_PATH = PARENT_DIR / "cliques.jsonl"
def main(
words_archive_path: Path = WORDS_ARCHIVE_PATH,
words_filename: str = WORDS_FILENAME,
cliques_path: Path = CLIQUES_PATH
):
"""
Load a list of words from a file (filename: word_filename)
within a zip archive (words_archive_path). Save a file with
all of the cliques (of mutually exlusive letters) to cliques_path.
"""
words = (
extract_archive_to_word_list(words_archive_path, words_filename)
| get_unique_set_words_of_length_n(5)
)
five_cliques = find_all_size_n_cliques(words, 5)
with jsonlines.open(cliques_path, 'w') as writer:
writer.write_all(five_cliques)
if __name__ == '__main__':
main()
Including the time to load in the data and construct the igraph.Graph, this script took 10.2 seconds on my 2019 Macbook Pro. In total, there were 538 five-word sets using 25 letters (ignoring anagrams).
Here’s a sampling of some of the word sets:
| chivw | enzym | fldxt | jakob | sprug |
| ampyx | crwth | fdubs | glink | vejoz |
| bortz | chivw | dunks | flegm | japyx |
Maybe I shouldn’t be surprised that these aren’t quite in the vernacular.
You can find the complete source for this post here.